|
4.Linguaggi per elaboratori e per persone Il millepiedi era tanto beato La storia del millepiedi è imbarazzante. Noi amiamo credere, di solito, che riflettere e capire siano,per definizione, le migiori cose da fare e che, in particolare, siano utili all'apprendimento. Ma il millepiedi finì male riflettendo sulle proprie azioni. La stessa cosa accadrebbe a noi? Questo significa che noi dovremmo smettere di pensare su noi stessi? In effetti nella nostra cultura "razionale", la nozione che il pensiero ostacola l'azione, e perfino che pensare impedisce d'imparare, prevale nettamente. Il nostro usuale modo di esprimerci sull'imparare ad andare in bicicletta: "Continua a provare, un giorno imparerai", è il tipico consiglio che i genitori danno ai bambini mentre si arrabbattano sulle due ruote. Molti filosofi hanno sviluppato l'idea che certe conoscenze non possono descriversi con parole, né essere afferrate dal pensiero cosciente. L'idea è stata inserita nelle recenti riforme dei programmi dai sostenitori dell'apprendimento attivo, con il supporto teorico della classificazione di J.S. Bruner ' dei processi cognitivi, che esercita una grande influenza: alcune conoscenze sono rappresentate come azioni, altre come immagini, e soltanto la terza categoria come simboli. Bruner ha asserito che "parole e diagrammi " sono " impotenti " a esprimere certe forme di conoscenza che solo l'azione potrebbe rappresentare. Io cerco, in questo capitolo, di sviluppare una prospettiva più flessibile su questi problemi. La mia prospettiva è più flessibile perché io rifiuto l'idea della dicotomia tra il verbalizzabile e il non vérbalizzabile. Nessuna conoscenza è completamente riducibile in parole, e nessuna conoscenza è interamente inesprimibile. La mia prospettiva è più flessibile anche perché considera una dimensione storica: una componente importante nella storia della conoscenza è l'evoluzione di tecniche che accrescono il potere di "parole e diagrammi". E ciò che è vero storicamente è anche vero per la singola persona: per chi vuole ampliare le sue conoscenze, è importante imparare ad estendere il confine di quanto si può esprimere con parole. Da questo punto di vista, la questione sulla bicicletta non è se si possa o no " dire " a uno " in modo esauriente " come si fa, ma piuttosto come migliorare la nostra abilità a comunicare con altri (e con noi stessi in dialoghi interiori) quanto basta per incidere sul modo d'imparare ad andare in bicicletta. Il tema centrale di questo capitolo è lo sviluppo di linguaggi descrittivi che permettano di parlare dell'apprendimento. Porremo particolare attenzione ad una delle maniere di apprendere che molti ritengono si realizzi meglio attraverso "il fare ": l'apprendimento di abilità fisiche. Il nostro approccio è esattamente l'opposto di come nelle scuole viene trattata l'educazione fisica in quanto materia non intellettuale. La nostra strategia consiste nel rendere chiaro perfino ai bambini che apprendere un'abilità fisica ha molto in comune con la costruzione di una teoria scientifica. Da questa impostazione derivano molti vantaggi. Primo, io so dal lavoro svolto nel laboratorio LOGO che le stesse abilità fisiche vengono apprese molto meglio.2 Senza questo vantaggio diretto, il cercare di " motivare" un'idea scientifica stabilendo un'analogia con un'attività fisica, potrebbe facilmente degenerare in un altro esempio di "verbosità didattica ". Ma se noi possiamo trovare un'onesta collocazione per il pensiero scientifico nelle attività che il bambino sente come importanti e personali, apriremo le porte a un modello di apprendimento più coerente e sintonico. In questo capitolo dimostro che ciò può essere realizzato e suggerisco che collegare la scienza alle abilità fisiche può fare molto di più, per l'apprendimento scientifico, che fornire una cosiddetta " motivazione ". Potenzialmente questo può mettere i bambini nella condizione di identificarsi, in certo qual modo, con gli scienziati, sapendo che gli scienziati usano linguaggi descrittivi formali e che anch'essi possono usare tali linguaggi come strumenti per apprendere abilità fisiche, per esempio giochi di destrezza. L'idea è di dare ai bambini un'occasione di pensare se stessi nell'atto di " fare scienza ", quando stanno facendo qualcosa di piacevole col loro corpo. Se i bambini potessero vedere le coordinate geometriche inventate da Cartesio come qualcosa di non totalmente estraneo alle loro personali esperienze quotidiane, questo non solo renderebbe Cartesio più significativo, ma, nello stesso tempo, li aiuterebbe a considerare se stessi più significativi. Ma vediamo più da vicino quello che pensa la nostra cultura sull'apprendimento delle abilità fisiche. Essa non è più coerente su questo argomento di quanto non lo sia riguardo ai più " astratti " contenuti matematici discussi prima. Sebbene la saggezza popolare e gran parte della psicologia dell'educazione concordino sul fatto che si tratta di un campo dove il pensiero cosciente non è d'aiuto, chi fa dello sport professionistico non sempre ne conviene. Alcuni dei migliori allenatori dedicano molto impegno ad analizzare e verbalizzare i movimenti che devono essere appresi e perfezionati. Un autore sportivo, Timothy Gallwey, ha tradotto la sensibilità popolare per questa contraddizione in un successo editoriale. Nel suo libro Inner Tennis egli dà alcuni suggerimenti per uscire da questo dilemma. Gallwey incoraggia colui che apprende a considerare se stesso come se fosse costituito da due personalità: una analitica e verbale, l'altra più olistica e intuitiva. E' opportuno, egli sostiene, che ora l'una ora l'altra di queste due personalità abbiano il comando. Una parte importante del processo d'apprendimento consiste nell'insegnare a ciascuna "personalità " a capire quando prenderlo e quando lasciarlo all'altra. La descrizione che Gallwey dà dei compromessi e delle transazioni che si accompagnano ad un apprendimento riuscito è insolita negli ambienti pedagogici. Egli lascia a colui che apprende piena libertà di scelta tra i modi di pensare analitico e olistico. Questo è molto diverso da ciò che awiene nell'elaborazione dei programmi scolastici. I riformatori di programmi sono spesso preoccupati di scegliere tra l'apprendimento verbale e non verbale. La loro strategia consiste nel fare questa scelta a monte, includendola nel programma. La strategia di Gallwey, invece, è di aiutare gli allievi a impa.rare a fare in proprio questa scelta: una prospettiva che è in linea con l'immagine già proposta del bambino epistemologo, dove il bambino è' incoraggiato a diventare esperto nel saper distinguere e scegliere tra i vari stili di pensiero. I1 fatto che io citi Timothy Gallwey non è un avallo di tutto quello che egli dice. Gran parte delle sue idee mi appaiono discutibili, ma penso che egli non sia lontano dal vero quando riconosce che, in merito all'apprendimento di abilità, noi abbiamo bisogno di modi di parlare e di pensare più strutturati. Il linguaggio d'oggi non è abbastanza ricco in questo campo. In un mondo pieno di elaboratori, senza dubbio saranno introdotti in tutta la nostra cultura linguaggi informatici che, contemporaneamente, forniranno un mezzo per servirsi dell'elaboratore e offriranno linguaggi descrittivi nuovi ed efficaci per pensare. Essi avranno un particolare effetto sul linguaggio che usiamo per descrivere noi stessi e il nostro apprendimento. In una certa misura ciò è già avvenuio: non è raro sentire delle persone senza alcuna conoscenza informatica, usare concetti quali input, output e feed-back per descrivere i loro processi mentali. A titolo di esempio, dimostreremo come i concetti della programmazione possano essere utilizzati in quanto struttura concettuale per imparare una particolare abilità fisica, vale a dire a fare giochi di destrezza. Consideriamo dunque la programmazione come fonte di metodi descrittivi: in breve, come un mezzo per rinforzare il linguaggio. Molti progressi scientifici e matematici hanno svolto una funzione linguistica similare, fornendoci parole e concetti per descrivere ciò che fino ad allora era sembrato troppo amorfo per il pensiero sistematico. Uno degli esempi più sorprendenti del potere dei linguaggi descrittivi è la genesi della geometria analitica, il cui ruolo fu cosl determinante nello sviluppo delle scienze moderne. Secondo la leggenda, Cartesio avrebbe inventato la geometria analitica osservando una mosca sul soffitto, la mattina tardi, mentre era a letto. Immaginiamo che cosa può aver pensato. La mosca, volando qua e là, tracciava una traiettoria tanto reale quanto i cerchi e le ellissi della matematica euclidea, ma tale che sfidava una descrizione in linguaggio euclideo. Fu allora che Cartesio intravvide un mezzo per afferrare il fenomeno: in ogni momento si poteva descrivere la posizione della mosca precisando a quale distanza si trovava dai muri. Si potevano descrivere i punti nello spazio con coppie di numeri; si poteva descrivere una traiettoria con un'equazione o una relazione verificata da quelle coppie di numeri i cui punti giacessero sulla traiettoria. La potenza dei simboli ha fatto un passo in avanti quando Cartesio scoprì come utilizzare un linguaggio algebrico per parlare di spazio, e un linguaggio spaziale per parlare di fenomeni algebrici. Il metodo delle coordinate cartesiane, nato da questa intuizione, ha cosl fornito strumenti che la scienza da allora ha usato per descrivere le traiettoria di mosche e pianeti e le traiettorie di oggetti più astratti, gli enti della matematica pura. La scoperta di Cartesio ha molto in comune con l'esperienza del bambino alle prese col cerchio Tartaruga. I1 bambino, ricordiamolo, stava esplicitamente cercando una via per descrivere come si cammina in cerchio. In LOGO, questa descrizione assume una forma molto semplice e il bambino ha da inventare solo la descrizione, mentre Cartesio ha dovuto fare ben di più. Ma in ambedue i casi la ricompensa è l'abilità di saper descrivere analiticamente qualcosa fino ad allora conosciuto in modo globale, percettivo-cinestetico. Né il bambino né Cartesio hanno subito la sorte del millepiedi: tutti e due hanno potuto camminare in cerchi, sia prima che dopo aver imparato a descrivere i loro movimenti analiticamente. Ma il formalismo di Cartesio, per quanto potente esso sia per descrivere i processi del mondo della fisica, non è adatto a descrivere i processi nel mondo dell'educazione fisica. Usare il calcolo per descrivere giochi di
destrezza o come cammina un millepiedi, provocherebbe confusione. Se si tentasse di
imparare qualche attività fisica con l'aiuto di tali descrizioni, quasi certamente ci si
ritroverebbe nel più vicino fossato, con la testa febbricitante. Questo metodo di
descrizione formale non è adatto al compito. Ma esistono altri formalismi. Nel campo
della ricerca pedagogica non si è ancora lavorato in questo senso. Ma un'altra comunità
di ricerca, quella degli informatici (per ragioni sue proprie), ha dovuto lavorare sul
problema dei linguaggi descrittivi diventando quindi una fonte inaspettata d'innovazione
educativa. Agli elaboratori si chiede di fare molte cose, e l'ordinare a un elaboratore di
fare qualcosa, richiede che il processo sottostante
sia descritto, a un certo livello, con sufficiente precisione perché sia eseguito dalla
macchina. Così gli informatici (computer scientists) hanno dedicato molto del loro
talento e della loro energia allo sviluppo di formalismi descrittivi efficaci. Si potrebbe
anche dire che la « scienza degli elaboratori » * sia così chiamata erroneamente: gran
parte di essa non è scienza degli elaboratori, ma scienza delle descrizioni e dei
linguaggi descrittivi. Alcuni dei formalismi descrittivi prodotti dall'informatica sono
esattamente quelli necessari per tenere sotto controllo il processo d'apprendimento di un
esercizio fisico. E' quello che qui dimostriamo scegliendo un importante nucleo teorico
della programmazione: il concetto di programmazione strutturata, che illustreremo con
l'esperienza d'apprendimento, in ambiente LOGO, di un bambino al quinto anno di scuola.
Ciò che apparve sullo schermo fu
l'inaspettato disegno di un « uomo non riuscito » (vedi Fig. 10c). Che cosa non andava?
Keith era preparato a sorprese di questo tipo. Il gruppo di concetti connessi a bugs e
debugging, l'abbiamo già detto, è uno dei pilastri dell'ambiente LOGO. Non ci si aspetta
che tutto funzioni al primo colpo. Non si giudica con i soliti « esatto, hai preso un
buon voto » e « sbagliato, hai preso un brutto voto ». Invece, ci si pone la domanda:
« Come posso aggiustarlo? », e si deve prima capire che cosa di fatto è successo. Solo
allora si potrà farlo riuscire come vogliamo noi. Ma in questa situazione Keith non era
capace di stabilire che cosa era successo. Aveva scritto il suo programma in modo tale che
era estremamente difficile mettere in evidenza il suo errore. Dov'era, dunque, il bug nel
suo programma?Quale errore aveva potuto provocare una trasformazione tanto forte delle sue
intenzioni? Per capire la sua difficoltà, confrontiamo il suo programma con una diversa
strategia di programmazione, conosciuta come «programmazione strutturata ». Il nostro
scopo è di suddividere il programma in parti semplici, per poter isolare e
rettificare gli errori separatamente in ciascuna parte. Mentre nella lunga, informe
sequenza di istrúzioni date da Keith, è difficile isolare un bug, lavorando su piccole
parti si può più facilmente circoscriverli ed evidenziarli. In questo caso, una
suddivisione del tutto naturale consiste nell'elaborare un programma per disegnare
un'entità a forma di V da usare per braccia e gambe, un altro programma traccerà il
quadrato della testa. Una volta che queste «sottoprocedure» sono state scritte e
verificate, è estremamente facile scrivere la « superprocedura » che ci darà la figura
stilizzata. Possiamo scrivere un programma molto semplice: Questa procedura è abbastanza semplice da afferrare nel suo insieme. Ma senza dubbio la sua semplicità deriva dal presupposto che l'elaboratore comprenda le istruzioni VI e TESTA. Altrimenti il passo successivo deve essere quello di definire VI e TESTA. Lo possiamo fare nello stile di sempre, preparando una procedura comprensibile nella sua globalità. Per esempio: PER VI (In questo programma assumiamodi aver definito l'istruzione
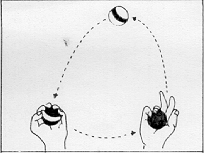
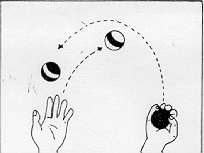
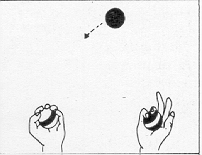
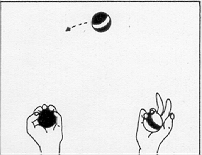
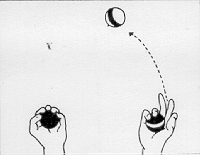
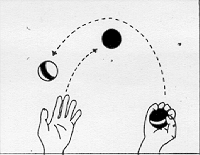
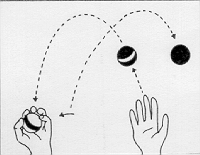
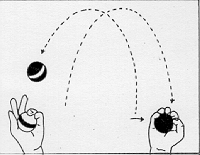
LINEA, che fa andare avanti e tornare indietro la Tartaruga.) PER LINEA :DISTANZA Robert, un allievo al settimo anno di scuola, espresse la sua conversione a questo stile di programmazione esclamando: « Vedete, tutte le mie procedure sono bocconi a misura di mente». Ha poi ampliato la metafora con altri commenti: «Prima ero solito confondermi con i miei programmi, ora non mordo più di quel che posso masticare». Aveva fatto, una scoperta fondamentale: si può costruire un vasto sistema intellettuale senza fare mai un passo che non sia stato ben compreso. E nello stesso tempo, il costruire con una struttura gerarchica permette di impossessarsi del sistema nel suo insieme, vale a dire di vedere il sistema come se fosse «guardato dall'alto ». A Keith, l'autore del programma non strutturato UOMO, era stata suggerita l'idea di utilizzare sottoprocedure, ma lui vi aveva opposto resistenza. La forma di programma lineare era più vicina al suo modo di fare le cose. Egli non aveva mai sentito un bisogno impellente di programmazione strutturata fino al giorno in cui non poté mettere a punto il suo programma UOMO. Nelle esperienze LOGO ciò è accaduto spesso. Quando un bambino si trova in situazioni simili e chiede che cosa deve fare, di solito è sufficiente dire: «Tu sai che cosa fare! ». E spesso il bambino dirà, talvolta trionfante, talvolta timido: « Penso che dovrei trasformarlo in sottoprocedure, vero? ». Il « modo giusto» non fu imposto a Keith; l'elaboratore gli offrì sufficiente elasticità e potenza perché le sue ricerche fossero naturali e personali. Questi due stili di approccio alla preparazione ed esecuzione di un progetto si possono applicare a qualunque situazione. Possiamo ritrovarli osservando gli stili di apprendimento sia di abilità «fisiche» che «intellettuali». Consideriamo, per esempio, due allievi del quinto anno di scuola che si esercitavano, nel nostro laboratorio, in attività sia di programmazione che fisiche. Michael è robusto, atletico, si considera «un duro ». Paul è introverso, studioso, di costituzione fisica esile. Michael è mediocre a scuola e Paul è bravo. Cosi, nessuno era sorpreso quando Paul migliorava velocemente nel lavoro all'elaboratore, avventurandosi in procedure di programmazione strutturata molto complesse. Dopo molte settimane, Michael era solo capace di scrivere programmi lineari. Senza alcun dubbio possedeva tutti i concetti necessari per scrivere programmi più elaborati, ma era trattenuto da una forte e tipica resistenza nell'utilizzare sottoprocedure. In questo stesso periodo tutti e due cominciarono a imparare a camminare sui trampoli. La tattica di Michael era di fissare nella sua mente un modello in forma sequenziale: a Un piede sulla sbarra, mi alzo, un piede sull'altra sbarra, il primo piede avanti... ». II primo tentativo sfociò in una rapida caduta, ma con coraggio Michael ricominciò una volta due volte e cosl via, fiducioso che finalmente ci sarebbe riuscito, e cosl accadde. Ma, con sorpresa di tutti e due, Paul c'era riuscito prima. La tattica di Paul era stata diversa. Aveva iniziato allo stesso modo, ma quando si era accorto che non faceva progressi, aveva cercato di isolare e correggere quella parte del metodo che gli procurava noie: il bug. Quando si avanza il piede per effettuare il primo passo, si tende a lasciare il trampolo dietro. Una volta identificato questo errore, non è difficile eliminarlo. Un espediente per arrivarvi sta nel pensare di fare il passo con il trampolo, invece che con il piede, e di lasciare che il trampolo a porti » il piede. Ciò si ottiene sollevando il trampolo col braccio contro il piede. L'analogia col suo approccio alla programmazione fu cosl evidente a Paul, che può essere stata una causa del «transfert» dalla programmazione all'apprendimento di questa attività fisica. In realtà è più probabile che tutte e due le situazioni derivassero da caratteristiche latenti nel suo generale atteggiamento cognitivo. Ma l'esperienza con LOGO rese Paul capace di articolare questi aspetti del suo atteggiamento. Nel caso di Michael, il rapporto tra la programmazione e l'allenamento con trampoli era ancora più evidente. Fu solo attraverso questa analogia che arrivò a riconoscere esplicitamente la differenza tra il suo metodo e quello di Paul. In altre parole, l'esperienza acquisita con la programmazione aiutò i due ragazzi a comprendere meglio le proprie azioni e ad avere un'opinione più articolata di se stessi. La validità generale dell'idea di programmazione strutturata presa come principio matetico, vale a dire come aiuto all'apprendimento, sarà ancora più evidente attraverso il prossimo esempio: si tratta del processo d'apprendimento di un'altra attività fisica, i giochi di destrezza. Non è un caso se lo scegliamo. Il cerchio Tartaruga si prestava all'apprendimento della matematica «col proprio corpo »; i giochi di destrezza si prestano altrettanto bene ad imparare un'attività corporea «con la matematica ». Naturalmente il quadro reale è complesso e più interessante, perché in ambedue i casi il processo opera in due direzioni, dalla metafora informatica al linguaggio corporeo e viceversa. Sperimentando la geometria della Tartaruga, i bambini affinano il senso che hanno dei loro corpi e dei loro movimenti, nonché la loro comprensione della geometria formale. I concetti teorici relativi ai programmi strutturali, tradotti in termini di giochi di destrezza, in termini realmente corporei, acquistano nuova concretezza ed efficacia. Nell'uno e nell'altro caso, la conoscenza assume la qualità che noi abbiamo chiamato «sintonica». Ci sono molti tipi di giochi di destrezza. Quando si pensa al giocoliere ci si riferisce a uno che compie esercizi di destrezza secondo una procedura detta « a pioggia ». In questo tipo di gioco, le palle si muovono una dietro l'altra in cerchio, passando da sinistra a destra in alto e da destra a sinistra in basso (o viceversa). Questo comporta due tipi di lanci: un lancio corto e basso, per far passare le palle da una mano all'altra nella parte bassa del cerchio (vicino alle mani), e uno lungo e alto, per far ruotare le palle seguendo la parte alta del cerchio (vedi Fig. 11). Il gioco «a cascata» ha una struttura più semplice. La parte inferiore del cerchio è assente; le palle circolano nelle due direzioni lungo l'arco superiore. Non c'è che un tipo di lancio: lungo e alto (vedi Fig. 11). La sua semplicità lo rende il migliore esercizio d'avviamento per l'apprendista giocoliere e nello stesso tempo l'esempio migliore per il nostro proposito. La domanda da porci è la seguente: chi vuole imparare il gioco troverà un aiuto o un ostacolo nella descrizione verbale e analitica di come farlo? La risposta è:
dipende. Dipende dagli strumenti di cui dispone l'apprendista giocoliere per fare descrizioni analitiche. Noi utilizziamo il gioco a cascata per dimostrare come dei buoni modelli per elaboratori possano aiutare a sviluppare «procedure umane» che migliorino delle prestazioni fisiche e come la riflessione su queste procedure possa aiutarci ad imparare a programmare e fare matematica. Ma è pur vero che certe descrizioni verbali rischiano di confondere invece di essere utili. Consideriamo, per esempioa la descrizione seguente: 1. Cominciare col mettere le palle 1 e 2 nella mano sinistra e la palla 3 nella mano destra. 2. Lanciare la palla 1 verso la mano destra, facendole descrivere una parabola alta. 3. Quando la palla 1 è al vertice, lanciare la palla 3 verso la mano sinistra facendole descrivere una parabola similare, ma fare attenzione a lanciare la palla 3 sotto la traiettoria della palla 1. 4. Quando la palla 1 arriva nella mano destra e la palla 3 è al vertice, afferrare la palla 1 e lanciare la palla 2 in modo che passi sotto la traiettoria della palla 3. e così via... Questa descrizione è sostanzialmente un brutale programma
lineare. Non può essere di alcun aiuto ad un apprendista giocoliere. Le persone estranee
alla cultura informatica potrebbero trovarlo molto simile a un programma d'elaboratore:
«proprio un'istruzione dopo l'altra ». Ricorda certi programmi, come quello del primo
UOMO di Keith. Ma abbiamo visto che allineare le istruzioni senza dar loro una valida
struttura interna non è neppure un buon metodo di programmazione, e constateremo che le
tecniche di programmazione strutturata che sono davvero efficaci Per scrivere programmi,
lo sono anche come descrizioni matetiche del gioco di destrezza. Le definizioni da introdurre saranno del tipo seguente: QUANDO qualcosa LANCIODESTRA Per riempire gli spazi non definiti, i « qualcosa »,
dobbiamo descrivere due condizioni, o due « stati » identificabili del sistema, che
daranno il via all'azione del lanciare.
Ma questa rappresentazione dello stato del sistema è
incompleta: non indica in quale direzione si muove la palla in alto. Per completarla,
aggiungiamo una freccia che indichi una direzione (Fig. 13a) e otteniamo due descrizioni
di stato (Figg. 13b e 13c). PER GIOCO_CONTINUO o ancora più semplicemente: PER GIOCO_CONTINUO Ora trasferiamo in una strategia didattica le nostre ipotesi e la nostra procedura umana. FASE 1: Verificare che l'apprendista giocoliere sia in grado di lanciare. Gli si dia una palla, gli si chieda di lanciarla nell'altra mano. In generale questo avviene facilmente, ma vedremo in seguito che spesso occorre rifinire, seppure di poco, il procedimento spontaneo, che comporta un bug. FASE 2: Verificare che l'apprendista sappia combinare i lanci Provare con due palle, dando per istruzioni: PER INCROCIO Lo scopo è di scambiare le palle tra mano sinistra e mano destra. Benché sembri una semplice combinazione di LANCIOSINISTRA e LANCIODESTRA, ciò non avviene quasi mai immediatamente Fase 3:Cercare i bugs nelle procedure di lancio. Perché PER INCROCIO non riesce? Normalmente ci si accorge che l'apprendista non sa lanciare cosl bene come sembrava nella fase 1. La difficoltà (bug) più comune deriva dal fatto che l'apprendista segue la palla con gli occhi, nel lanciarla. Poiché abbiamo solo un paio d'occhi, il primo lancio li impegna a tal punto da rendere il secondo quasi impossibile e di solito le palle finiscono disastrosamente a terra. Fase 4: Operazione di debugging. Se il bug consiste nel seguire la prima palla con gli occhi, vi si ovvia riportando l'apprendista a lanciare una sola palla senza guardarla. La maggior parte dei debuttanti scopre (con grande sorpresa) che basta poco esercizio per essere capaci di edattare un lancio, se si fissa lo sguardo attorno al previsto apice della parabola descritta dalla palla in movimento. Quando il lancio singolo è stato perfezionato, l'apprendista prova di nuovo a combinare i due lanci. Molto spesso la cosa ora funziona, sebbene possa esserci ancora un altro errore da eliminare. Fase 5:Si passa a tre palle. Una volta che l'apprendista giocoliere sa eseguire senza difficoltà la procedura che abbiamo chiamato INCROCIARE, si può affrontare questo stadio. Cominciare con due palle in una mano e una nell'altra (Fig. 14).
Varianti di questa strategia didattica sono state utilizzate da molti insegnanti LOGO. Uno di loro, Howard Austin, le ha studiate in modo particolareggiato e ha fatto oggetto della sua tesi di dottorato l'analisi di questo gioco. Non ci sono dubbi che la strategia sia molto efficace e c'è poco da dubitare anche riguardo al motivo: L'uso dei concetti della programmazione come linguaggio descrittivo facilita la ricerca e l'eliminazione degli errori (debugging). Nel descrivere il disegno di una figura stilizzata e l'apprendimento del gioco di destrezza, il nostro tema centrale era che il debugging è facilitato da una descrizione appropriata dei procedimenti complessi. Nei due casi, la descrizione riflette una rappresentazione del processo in una forma modulare, vale a dire frazionata in unità del tutto naturali e funzionali e la caccia al bug diventa agevole, avendolo circoscritto entro singoli passaggi semplificati al massimo. Le peggiori condizioni di caccia all'errore si hanno quando molti bugs si presentano contemporaneamente: conviene che le unita modulari siano tanto ridotte da rendere improbabile che questo si verifichi. Le difficoltà causate da bugs molteplici sono ben illustrate da quello che accade ai principianti quando cercano di imparare un gioco di destrezza affrontandolo brutalmente. In effetti spesso ci riescono (come Michael era riuscito a camminare sui trampoli), generalmente dopo ore di tentativi frustranti per mantenere tre palle in aria senza essere neppure capaci di farne incrociare due. Ma ci mettono molto tempo per imparare. Quando Howard Austin studiò più da vicino le azioni del principiante, notò gli stessi bugs che abbiamo rilevato nella nostra strategia razionale, per esempio, quello che consiste nel seguire la palla con gli occhi. A forza di ripetizioni, il cosiddetto «apprendimento per tentativi ed errori», finiva col produrre un comportamento efficace. Per puro caso, durante un lancio capiterà che gli occhi si muovano un po' meno. Gli esseri umani, come altri animali, sono dotati di meccanismi d'apprendimento capaci di captare questi momenti e di accrescere la probabilità che si ripetano. Infine, gli errori sono eliminati e il soggetto impara il gioco di destrezza. Le persone sono capaci di imparare allo stesso modo dei topi in un labirinto. Ma il processo è lento e primitivo. Possiamo imparare di più, e più in fretta, se acquisiamo un controllo consapevole del processo d'apprendimento, articolando e analizzando il nostro comportamento. Se le procedure di tipo informatico migliorano l'apprendimento, non ne consegue che si possano sopprimere, come per magia, tutti i processi ripetitivi che ogni acquisizione esige o che si possa ridurre a quasi niente il tempo necessario per imparare i giochi di destrezza. Ci vuole tempo per trovare i bugs ed eliminarli, come per raggiungere le diverse abilità necessarie. Ciò che si potrà eliminare, invece, sono i metodi dispendiosi e inefficienti. Quando il metodo d'apprendimento è povero, bisogna esercitarsi per ore ed ore prima di saper giocare con tre palle correttamente. Quando è buono, il tempo è di gran lunga ridotto: spesso sono sufficienti venti o trenta minuti. I bambini, molte volte, oppongono una resistenza alla ricerca degli errori analoga a quella che abbiamo riscontrato per le sottoprocedure. L'ho osservato durante i primi incontri di bambini con l'ambiente LOGO. Il bambino decide di far tracciare alla Tartaruga una certa figura, per esempio una casa o un uomo stilizzato. Un programma è presto scritto e provato. Non funziona. Invece di essere corretto, viene cancellato. Talvolta l'intero progetto è abbandonato. In altri casi, il bambino s'intestardisce, prova, riprova e riprova con ammirevole costanza, ma sempre ripartendo da zero, nelI'evidente tentativo di riuscire di un sol colpo. Il bambino può fallire o riuscire a far disegnare la figura all'elaboratore, ma non è certo riuscito ad acquisire la strategia di correzione (debugging). È ben comprensibile. L'etica scolastica se n'è lavata le mani. Ciò che noi riteniamo un buon programma con un piccolo bug, il bambino lo considera come « sbagliato », «cattivo» «nullo». La scuola insegna che gli errori sono male; l'ultima cosa che uno desidera è di andarli a cercare, di soffermarcisi o di pensarci su. Il bambino è felice di utilizzare l'opportunità che gli offre l'elaboratore di cancellarli senza che ne resti traccia per lo sguardo altrui. La filosofia del debugging suggerisce un atteggiamento opposto. Gli errori ci aiutano perché ci guidano a studiare ciò che è accaduto, a capire che cosa non andava e, attraverso la comprensione, a sistemare le cose. L'esperienza della programmazione, più di qualsiasi altra attività, porta i bambini a «credere » in questa filosofia. Il contatto con l'ambiente LOGO smuove gradualmente le tenaci resistenze a operare correzioni e a servirsi di sottoprocedure. Alcune persone che osservano la crescente tolleranza dei bambini per i loro « errori », attribuiscono la trasformazione d'atteggiamento agli insegnanti LOGO che sono pragmatici e possibilisti davanti ai programmi che i bambini considerano « sbagliati ». Io penso che, a ben vedere, c'è qualcosa di più sostanziale ancora. Nell'ambiente LOGO, i bambini imparano che anche l'insegnante è un allievo e che ciascuno di noi apprende dagli errori. ¶ Un gruppo di dodici allievi del quinto anno lavorava all' esperienza LOGO per molte ore alla settimana, dall'inizio del semestre di settembre. Ai primi di dicembre, il gruppo decise di lanciarsi in un progetto collettivo. Una Tartaruga meccanica sarebbe stata programmata per scrivere «Buon Natale» su delle immense bandiere di carta da appendere nei corridoi della scuola. Un progetto ideale. Le lettere dell'alfabeto furono divise tra i membri del gruppo. Ognuno doveva scrivere programmi per due o tre lettere, per disegni decorativi e per messaggi interi, utilizzando i programmi lettera come sottoprocedure. Ma tempeste di neve e altri inconvenienti ritardarono il lavoro; così arrivò l'ultima settimana di scuola e le bandiere non erano ancora state preparate. L'istruttrice responsabile del gruppo decise di infrangere le regole abituali e di preparare lei stessa parte della programmazione. Lavorò a casa senza Tartaruga e quando arrivò il giorno dopo, aveva una collezione di programmi da correggere: lei e i bambini avrebbero lavorato insieme. L'istruttrice e un bambino, seduti per terra, guardavano la Tartaruga che stava disegnando qualcosa che doveva essere la lettera R, ma la battuta obliqua era messa fuori posto. Dov'era la causa dell'errore? Mentre tutti e due cercavano di riflettere. il bambino ebbe una rivelazione: « Ma allora » disse a tu non sai davvero come correggerlo? ». Il bambino non sapeva ancora come dirlo, ma quello che lo stupiva era che sia lui che la sua insegnante si erano impegnati insieme in un progetto di ricerca. Questo aneddoto fa riflettere. Ci fa pensare a tutte le occasioni in cui questo bambino si è sentito dire dal maestro « facciamolo insieme », ben sapendo che la collaborazione era finta. La scoperta non può essere un gioco truccato; I'invenzione non può essere preordinata. Nelle scuole tradizionali, gli insegnanti cercano veramente di lavorare in collaborazione con i bambini, ma di solito è la materia stessa che non genera problemi di ricerca. Un adulto e un bambino possono collaborare in modo genuino sull'aritmetica della scuola elementare? Una caratteristica molto importante del lavoro con l'elaboratore è che l'insegnante e l'allievo possono essere coinvolti in una vera collaborazione intellettuale; insieme possono tentare di far fare all'elaboratore questo o quello e di capire ciò che esso sta facendo. Si presentano spesso situazioni nuove che né l'insegnante né il bambino avevano incontrato prima, cosicché l'insegnante non deve fingere di non sapere. Condividere il problema e l'esperienza della sua soluzione permette al bambino di imparare dall'adulto non « facendo quello che il maestro dice », ma « facendo quello che il maestro fa ». E una delle cose che il maestro fa è di ostinarsi su un problema fino ad averlo interamente compreso. L'ambiente LOGO ha di speciale che può fornire numerosi problemi che i bambini di scuola elementare riescono a comprendere con una completezza che è rara nella vita quotidiana. Per approfondire questo punto, può essere utile riesaminare i semplici esempi di ricerca d'errori già discussi. Abbiamo visto il programma: PER CASA PER TRIANGOLO Ma questo programma contiene un bug e traccia il triangolo dentro il quadrato anziché sopra. Perché? Sulle prime, a un bambino potrebbe sembrare un mistero. Ma si può immaginare « perché la Tartaruga ha fatto questa sciocchezza » seguendo il consiglio euristico ben noto: gioca alla Tartaruga. Fallo da te, ma fingi di essere sciocco come lei. Scoprire perché la Tartaruga ha fatto così, suggerisce quasi immediatamente una soluzione. Alcuni, per esempio, dicono: «La Tartaruga ha girato dentro il quadrato perché TRIANGOLO dice GIRA DESTRA». Un rimedio semplice (uno dei tanti possibili) è implicito in questa diagnosi: stabilire una procedura per il triangolo con rotazioni a sinistra. Ugualmente un adulto che pensasse di poter far tracciare alla Tartaruga un triangolo con RIPETI [AVANTI 100 DESTRA 60], avrebbe la sorpresa di veder apparire un esagono. Ma è possibile « entrare » nel programma e scoprire perché questo avviene. Inoltre, si può riflettere e scoprire che lterrore deriva da una comprensione molto superficiale del più comune enunciato del teorema d'Euclide sui triangoli: « la somma degli angoli di un triangolo è 180 gradi ». Il bambino (e senza dubbio anche la maggior parte degli adulti), vive in un mondo in cui ogni cosa è capita soltanto in parte: abbastanza bene forse, ma mai completamente. Per molti, è un'esperienza rara, forse unica, comprendere l'azione della Tartaruga tanto a fondo che non ci sia più nulla da dire in proposito. Per alcuni è un'esperienza esaltante: lo si vede dall'ardore con cui i bambini spiegano quanto hanno compreso. È per tutti un esempio chiarificante di conoscenza analitica, migliore di quello che la maggioranza della gente potrà mai incontrare. Il lettore potrebbe obiettare che, lungi dal comprendere tutto della Tartaruga, un bambino programmatore difficilmente capisce i complessi meccanismi all'opera dietro le quinte, ogniqualvolta una Tartaruga esegue un comando LOGO. Infatti, non rischiamo di ingannare i bambini ponendoli in un ambiente di tecnologia sofisticata, le cui complessità sono solo parzialmente comprese dagli specialisti d'informatica? Tali dubbi ci riconducono direttamente alle problematiche iniziali di questo capitolo. Io ho proposto, a titolo di esempio, una descrizione del gioco di destrezza nella forma di un semplice programma. Ma sorge la stessa perplessità: la descrizione in linguaggio procedurale coglie l'essenza dell'azione del giocoliere, oppure è una mistificazione che ne dissimula la complessità? Questi interrogativi sono universali e toccano istanze fondamentali del metodo scientifico. Newton « capì » I'universo riducendo tutti i pianeti a punti che si muovono secondo un insieme invariabile di leggi del moto. Così facendo, egli coglieva l'essenza del mondo reale, oppure ne minimizzava le complessità? In parte, essere capace di pensiero scientifico significa avere una comprensione intuitiva di tali questioni epistemologiche e credo che il lavoro con la Tartaruga fornisca ai bambini l'opportunità di venirne a conoscenza. In realtà i bambini capiscono subito che la Tartaruga definisce un universo chiuso, in cui certe questioni sono pertinenti e altre no. Nel capitolo seguente parlerò di come quest'idea possa essere sviluppata grazie alla costruzione di molti altri « microcosmi », ciascuno con le sue ipotesi e le sue restrizioni. I bambini giungono ad apprezzare l'esplorazione delle proprietà di un dato microcosmo, senza essere disturbati da questioni estranee; in tal modo imparano a trasferire gli abituali atteggiamenti di esplorazione dalla propria vita quotidiana all'ambito formale dell'elaborazione di teorie scientifiche. L'intelligibilità interna dei mondi informatici offre ai bambini la possibilità di realizzare progetti di una complessità maggiore di quella normalmente possibile nel mondo fisico. Molti bambini immaginano di poter edificare complesse strutture con un gioco di costruzioni, oppure fantasticano di organizzare un gruppo di amici per grandiose imprese, ma quando tentano di realizzare i loro progetti, ben presto si scontrano con i limiti imperscrutabili delle cose e delle persone. Proprio perché i programmi d'elaboratore, per principio, possono essere fatti agire esattamente come nelle intenzioni, è possibile combinarli con maggiore soddisfazionc in sistemi complessi. Perciò i bambini sono in grado di sentirsi a loro agio nella complessità. La scienza moderna e l'ingegneria ci hanno dato l'opportunità di realizzare progetti con un grado di complessità fino a ieri difficilmente immaginabile. Ma la scienza ci insegna anche il potere della semplicità e io termino il capitolo con la storia, a mio parere commovente, di una bambina che ha imparato qualcosa del genere, in un'esperienza particolarmente semplice ma personalmente importante. Deborah era al sesto anno e aveva dei problemi a scuola; fu introdotta nel mondo delle Tartarughe da schermo, e le fu mostrato come esse ubbidivano ai comandi AVANTI, SINISTRA e DESTRA. Molti bambini trovano una piacevolissima fonte di potere e uno stimolante campo di esplorazione il fatto che a questi comandi si possa abbinare qualsiasi numero. Deborah lo trovò terrificante: la stessa reazione che aveva per la maggior parte delle attività scolastiche. Nelle sue primissime ore di lavoro con la Tartaruga, mostrò un'assillante dipendenza dall'istruttore, chiedendo costantemente rassicurazioni prima di intraprendere il più piccolo passo esplorativo. Si ebbe una svolta quando Deborah decise di limitare i suoi comandi, creando un microcosmo nel microcosmo dei comandi Tartaruga. Si permise solo un comando di rotazione: DESTRA 30. Per far girare la Tartaruga di 90 gradi, doveva ripetere tre volte DESTRA 30 e doveva ripeterlo undici volte per ottenere l'effetto di SINISTRA 30. A un osservatore poteva sembrare noioso ottenere degli effetti tanto semplici in un modo cosl complicato; ma Deborah era entusiasta di riuscire a costruire il suo personale microcosmo e a scoprire tutto quello che poteva fare entro le sue rigide limitazioni. Non chiese più conferme per provare. E un giorno, quando l'insegnante si offrì di mostrarle un « modo più semplice » per raggiungere un risultato, lei ascoltò pazientemente e disse: « Non credo che farò così ». Ne venne fuori quando fu pronta, molte settimane dopo, con un nuovo senso di fiducia che esibì non solo in più ambiziosi progetti Tartaruga, ma anche nell'affrontare qualsiasi altra cosa a scuola. Mi piace vedere nell'esperienza di Deborah un piccolo riassunto del processo storico avviato da pensatori come Copernico e Galileo, che ha permesso agli uomini di affrancarsi da superstizioni che nulla avevano a che fare con la fisica. In entrambi i casi, nella storia personale di Deborah e nella storia del pensiero occidentale, il successo di una teoria matematica non ha semplicemente avuto una funzione strumentale: esso è stato un'affermazione del potere delle idee e del potere della mente. Seymour Papert, MIND STORMS, bambini, computers e creatività |
||||||||||||||||||||||||||