Fiocco di neve classico generato dal triangolo equilatero
per iterazioni successive di merletti di Koch estroversi

Animazione esplicativa 
Livello 0. Triangolo equilatero. Poligono equilatero di 3 lati. Lunghezza lato: 1 (unitą di misura lineare) . Perimetro 3. Area:  1 (unitą di misura della superficie. Notare che se si volesse mantenere invece l'unitą lineare l'area risulterebbe 1/4 della radice di tre, valore per cui si dovrebbero moltiplicare i numeri relativi alle aree di seguito indicati).    Livello 1. Poligono equilatero di 12 lati. Lunghezza di un lato: 1/3. Perimetro 4. Area 4/3 (al precedente si sommano 3 piccoli equilateri di area 1/9)
Livello 2. Poligono equilatero di 48 lati. Lunghezza di un lato: 1/9. Perimetro 16/3. Area  40/27 (al precedente si sommano 12 piccoli equilateri di area 1/81) Livello 3. Poligono equilatero di 192 lati. Lunghezza di un lato: 1/27. Perimetro 64/9. Area  376/243 (al precedente, si sommano 48 piccoli equilateri di area 1/729)
Livello n. Poligono equilatero di 3*4n lati. Lunghezza di un lato: 1/3n. Perimetro 3*4n/3n.Area  ,,, (al precedente si sommano 3*4n-1 piccoli equilateri di area 1/9n) Livello infinito. All'infinito, passando al limite, si ottiene il classico fiocco di neve di Koch Poligono equilatero di infiniti lati. Lunghezza di un lato: infinitesima. Perimetro infinito. Area  8/5,

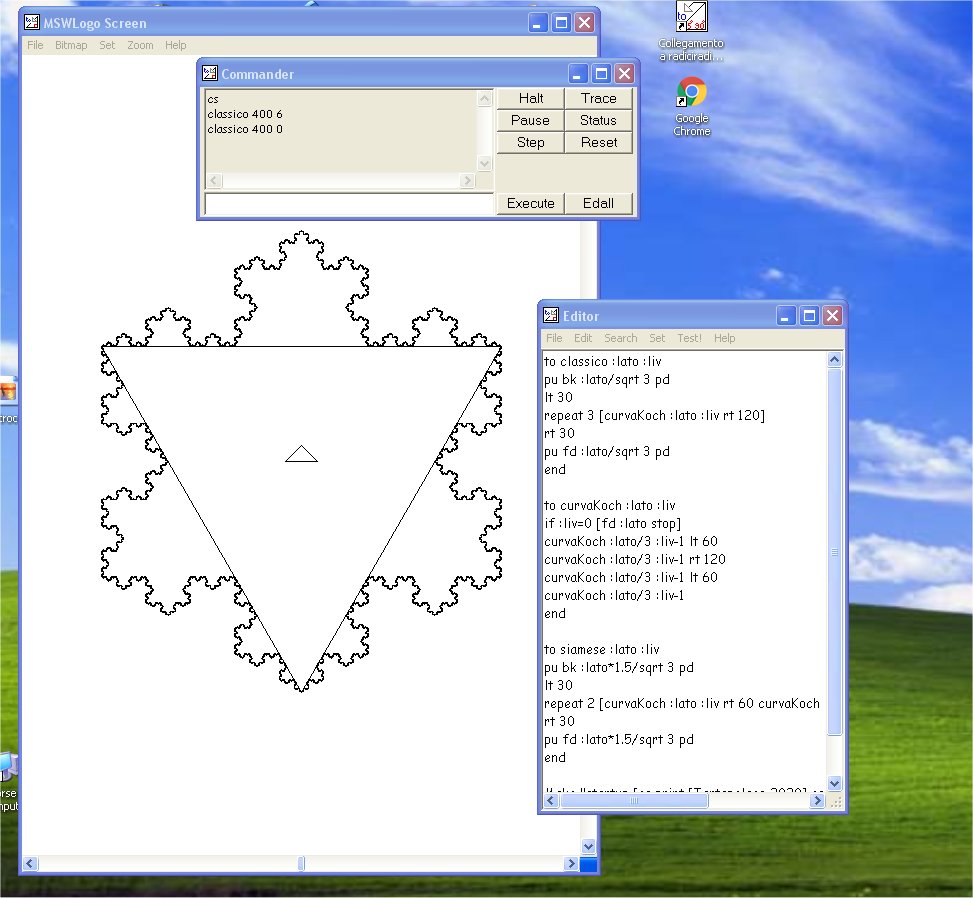
Le tre finestre dell'MSWLogo sulla sfondo di Windows. Nella finestra Editor le istruzioni per la tartaruga. Nella finestra Commander il comando per ottenere il fiocco di Koch e il suo triangolo generante che la tartaruga disegna nella finestra MSWLogo screen

Se non avete ancora MSWLogo potete scaricarlo dal sito della Softronix oppure cliccando qui.
Per avere il programmino potete copiarlo oppure scaricarlo cliccando qui
Il programma, scaricabile in formato zip, appena decodificato in formato LGO e caricato con "load" nel MSWLogo eseguirą automaticamente la lista di comandi assegnati mediante "make" alla variabile speciale "startup" leggibile nell'edit dopo i normali comandi per la tartaruga implementati dall'utente. Per il significato dei comandi utilizzati vedere anche il vocabolario animato del Tartapelago.