|
6. tangente e arcotangente |
|
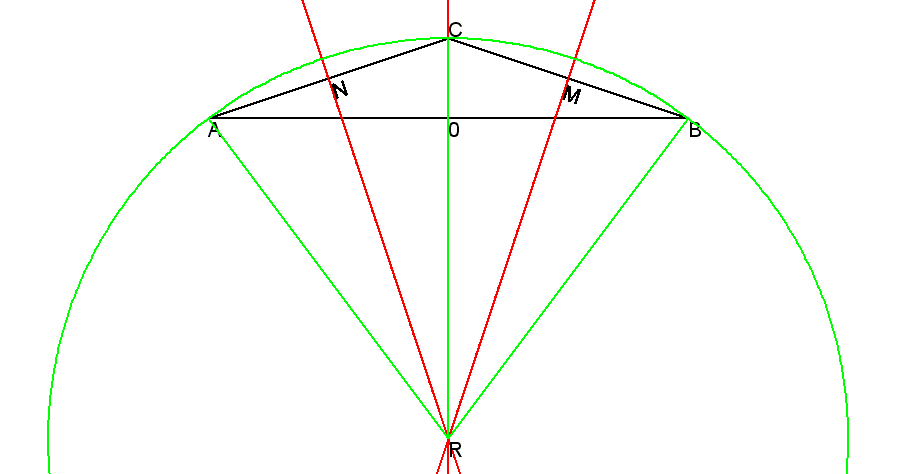
Triangoli simili, cioè con i tre angoli rispettivamente uguali, hanno uguale il rapporto tra lati corrispondenti. In particolare triangoli rettangoli simili hanno uguale il rapporto tra i cateti. Per esempio (4-osservazioni) abbiamo già visto che essendo CBO=CRM, per la similitudine tra i triangoli rettangoli COB e CMR, risulta CO/OB=CM/MR Dunque, in generale, in un triangolo rettangolo qualsiasi, ad una stesso rapporto di cateti corrisponde sempre lo stesso angolo e viceversa. La funzione che porta dall'angolo al rapporto dei cateti si chiama tangente (abbreviata spesso in tan). La sua inversa che porta dal rapporto dei cateti all'angolo si chiama arcotangente (abbreviata spesso in arctan) |
| Ad
esempio i triangoli rettangoli isosceli (metà quadrato) hanno 1 per rapporto
dei cateti e angolo opposto a un cateto uguale a metà retto, 45 gradi
o pigreco/4 radianti, quindi, usando i radianti e mettendo tra
parentesi, dopo la funzione il valore di partenza si ha tan(pigreco/4)=1 e, viceversa, arctan(1)=pigreco/4 Ricordiamo che l'angolo di 45 gradi (mezzo retto) in radianti è misurato da un arco di 1/8 (=45/360) di circonferenza di raggio 1 e, dunque, 2*pigreco*1/8=pigreco/4 |
|
Quindi finalmente siamo
in grado di esprimere l'angolo opposto a CM (uguale all'angolo opposto
a CO) scrivendo
Angolo CRM=arctan(CO/OB)
|
 |