|
Ultimo aggiornamento: 27/05/2005 |
|||||
|
Paolo Zellini "GNOMON (Una indagine sul numero)", Ed. Adelphi Milano, 1999 Lo "gnomone", preso in considerazione nel libro, non è quell'asticciola la cui ombra serve a segnare le ore negli orologi solari, o meridiane, ma è precisamente una figura geometrica, piana o solida, che Erone di Alessandria, ad esempio, definiva, in generale, come ciò che "aggiunto a qualsiasi entità, numero o figura, rende il tutto simile all'entità a cui è stato aggiunto." Filolao afferma: "Il numero è la forza sovrana autogenetica, che mantiene l'eterna permanenza delle cose del cosmo." Il concetto pitagorico, relativo al numero considerato secondo la natura dello gnomone, è ripetuto più volte nel testo. Nell'antichità, i concetti matematici erano stati pensati come un "logos divino", perché il loro potere di rendere uguale il diverso appariva decisamente straordinario. Lo gnomone era uno strumento matematico usato per la generazione di figure simili. Era diffusa tale tecnica, che rispondeva "all'esigenza di ingrandire o rimpicciolire una forma, conservandone l'aspetto." In questo modo si poneva "una delle più alte e ardue questioni della matematica e del pensiero in genere: quella dell'invarianza nel mutamento." Tale invarianza nel mutamento rappresenta un tema centrale degli Sulvasutra (trattati indiani) e dei passi dello Satapatha Brahmana, che analizzano le misure degli altari, i quali erano soggetti a successivi ingrandimenti, rimanendo invariata la forma. Paolo Zellini analizza la "matematica antica", mettendo a confronto le tradizioni mesopotamica, greca, egizia, indiana e cinese (trovando evidenti somiglianze), per "attraversare poi la matematica araba e l'algebra moderna, e sfociare infine in quel grandioso progetto che, dalla metà del XX secolo, ha visto entrare in scena la macchina come protagonista del calcolo su larga scala." Il libro rivela l'impegno dell'autore ad analizzare l'essenza del numero, cercando di rispondere alla famosa domanda di Didekind (con la quale la Premessa ha inizio): "Che cosa sono e che cosa vogliono significare i numeri?" Ringrazio Giorgio Pietrocola, che nel forum dell'Indire (corso ForTic B) ci ha regalato varie animazioni, costruite con la "tartaruga" del Logo; ne inserisco sette, citando alcune frasi di Giorgio stesso:
Ringrazio nuovamente Giorgio Pietrocola, che continua "La fiaba dello gnomo", riassumendo anche la "puntata precedente", per sottolineare determinati particolari, squisitamente matematici: "Gnomo, il rettangolo aureo tutto nero, di lato maggiore phi con esponente 0, cioè di lato maggiore: 1, e di lato minore phi con esponente 1, cioè di lato minore: 0,618..., e quindi di area phi, viene invaso da infiniti quadrati rossi che occupano il suo spazio, riducendolo a un infinitesimo. Poiché le dimensioni di Gnomo si riducono ogni volta di phi (circa 62%), i quadrati rossi hanno tutti delle aree pari alle potenze di phi con esponente 2; 4; 6; 8...(phi^2; phi^4...) e così via, mentre le aree delle varie forme di Gnomo corrispondono a phi con esponente dispari: 3; 5; 7; 9...(phi^3; phi^5...) e così via verso l'infinitamente piccolo."
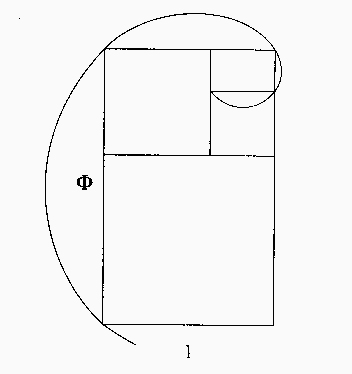
Nelle pagine 177 e 178, del libro "Gnomon", si legge: "Il numero F=(1 + Ö5)/2 può essere anche individuato da un'antanairesis rappresentabile in una sequenza illimitata, spiraliforme, di rettangoli simili. Se si considera il rettangolo di base 1 e altezza (1 + Ö5)/2, da questo si possono <<ritagliare>> tanti quadrati quante sono le volte che 1 è contenuto in (1 + Ö5)/2. Rimane come <<resto>> un rettangolo simile al primo, cui si applica la stessa operazione... Il processo è visibile in una successione illimitata di rettangoli simili...dove ognuno dei quali differisce dal precedente per via di uno gnomone formato dal quadrato costruito sul lato più grande. Si può così affermare che il quadrato è lo gnomone di un rettangolo aureo, cioè di un rettangolo tra i cui lati c'è un rapporto uguale a (1 + Ö5)/2. Ciò non dimostra che i pitagorici fossero in grado di ricavare con questa strategia una convergente al numero aureo, ma solo che il rapporto corrispondente al numero aureo poteva essere direttamente associato a un processo iterativo di successive correzioni gnomoniche.";
Cliccando su ciascuna immagine, inserita a sinistra in questo spazio, dedicato al libro "Gnomon", potrete vederla ingrandita. Per ritornare, poi, in questa pagina, basta cliccare sul pulsante "CHIUDI", che si trova in fondo a ciascuna pagina contenente l'immagine.
Nel libro "Gnomon", a pagina 33, si legge: "...Erone di Alessandria notò che in un qualsiasi triangolo se ne può ritagliare una parte che sia lo gnomone dell'altra. Ad esempio, in un triangolo isoscele con un angolo di 36 gradi e gli altri di 72 si può tracciare la bisettrice di uno degli angoli alla base in modo da ottenere due triangoli isosceli, uno simile a quello iniziale, e l'altro uguale allo gnomone del primo. L'operazione si può iterare all'infinito, ottenendo un'immagine a cui è sovrapponibile una curva a spirale...>>
|
|||||
|
AGGIORNAMENTO (19/06/04)
- L'immagine del rettangolo aureo "non canonico" (tratta dal libro "Gnomon"
di Paolo Zellini, a pag.177) ha destato curiosità e attenzione e nel forum
di base cinque abbiamo discusso in merito sia alla "spirale interna" sia a
quella "esterna". Grazie al rettangolo aureo Zelliniano, (nel quale la particolare disposizione dei quadrati è dovuta, forse, a una distrazione tipografica?) sono nate idee nuove e costruzioni interessanti. Credo che proprio evitando di seguire sempre e soltanto strade già percorse, si possano raggiungere traguardi imprevisti e sorprendenti... Ringrazio moltissimo - Gianfranco Bo (di cui segnalo la pagina web: http://utenti.quipo.it/base5/geopiana/spiraurea.htm per visionare l'articolo inerente a "La spirale aurea");
- Elena Saccardi, che ha preparato la
costruzione, visionabile sia nella pagina web di base cinque, già
precedentemente linkata, sia nell'animazione di Giorgio Pietrocola. |
|||||
|
AGGIORNAMENTO (22/06/04)
-
Tramite un'opportuna animazione, Giorgio
Pietrocola (che continuo a ringraziare) scrive: "Ho voluto
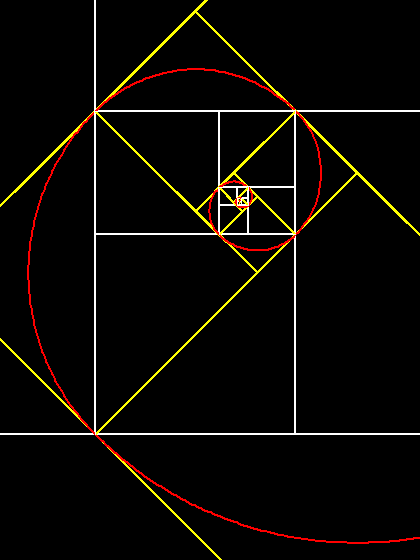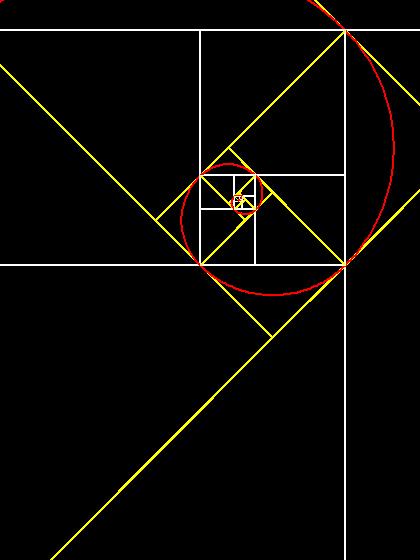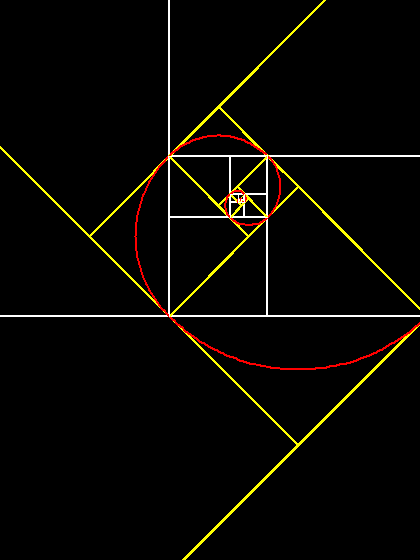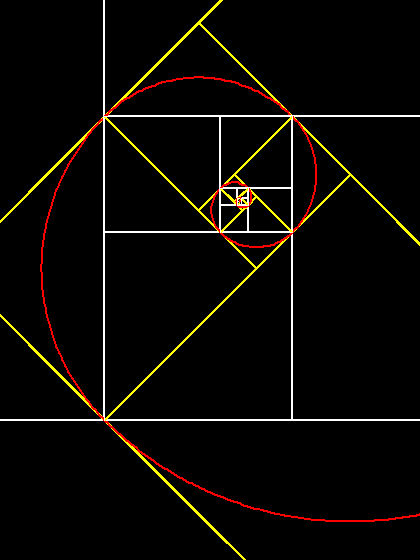
mettere a confronto le due seguenti costruzioni: - la costruzione, (eseguita da Dino, per visualizzare una bella "spirale approssimativa" del rettangolo aureo, precisamente una "poligonale" di archi di cerchio), che si ottiene puntando il compasso alla metà del lato opposto del rettangolo e tracciando l'arco, che passa per i due vertici del lato corrispondente ( in arancione nell'animazione); - la costruzione (eseguita da Elena), in cui, invece, si punta il compasso su un vertice di ogni quadrato "gnomone", con un'apertura pari alla misura del lato del quadrato stesso (in rosso nella stessa animazione). 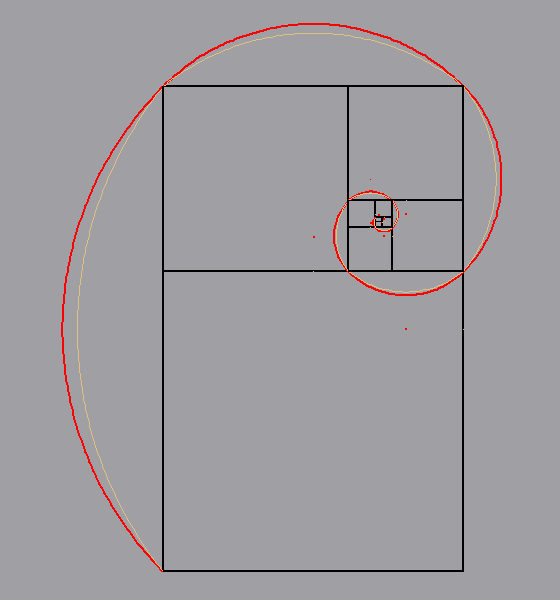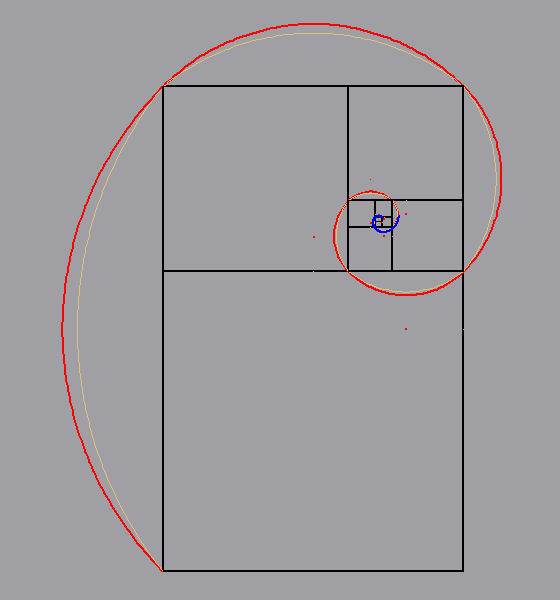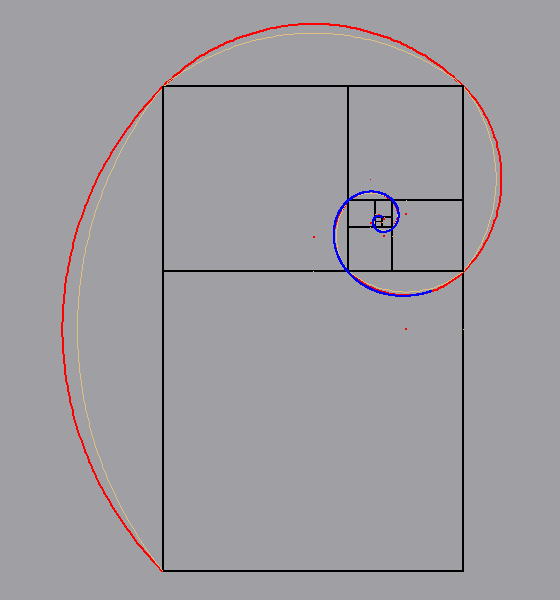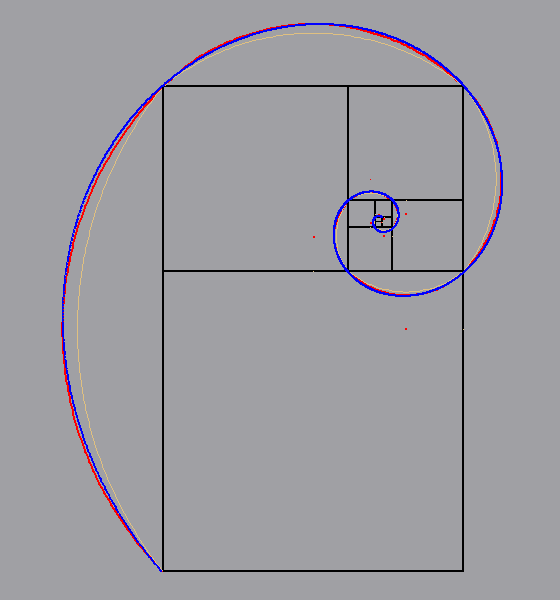 Il
risultato non sembra lasciare dubbi: la costruzione di
Elena è pressoché una spirale logaritmica perfetta... (clicca
sull'immagine per ingrandirla)" Il
risultato non sembra lasciare dubbi: la costruzione di
Elena è pressoché una spirale logaritmica perfetta... (clicca
sull'immagine per ingrandirla)"Dino Liberatore (che nuovamente ringrazio) conclude: "Aggiungo una curiosità: si può notare come una serie geometrica di rettangoli aurei sempre più piccoli converga intorno al punto, senza mai raggiungerlo  , (punto che si ottiene tracciando, in ciascuna coppia
di rettangoli,"genitore" e "figlio", le diagonali intersecantesi), chiamato
"l'occhio di Dio" dal matematico Clifford A. Pickover, che si è ispirato
alle proprietà <<divine>>, attribuite al rapporto aureo.".
Ecco l'immagine: clicca a destra per visualizzare l'occhio di Dio. , (punto che si ottiene tracciando, in ciascuna coppia
di rettangoli,"genitore" e "figlio", le diagonali intersecantesi), chiamato
"l'occhio di Dio" dal matematico Clifford A. Pickover, che si è ispirato
alle proprietà <<divine>>, attribuite al rapporto aureo.".
Ecco l'immagine: clicca a destra per visualizzare l'occhio di Dio.AGGIORNAMENTO (25/06/2004) - Giorgio Pietrocola, che nuovamente ringrazio, ha preparato alcune pagine web relative a un suo pregevole approfondimento, inerente allo "Studio di poligonali regolari aventi lati in progressione geometrica e delle relative curve interpolanti, eseguito con l' aiuto della fida tartaruga e della sua geometria.". Clicca qui per visitarle. |
|||||
|
Giorgio Pietrocola, che ringrazio ancora, ci offre, nell'ordine, sette costruzioni presentandole così : "Prima animazione: tra tutti i triangoli scaleni possibili quello che si incastra è unico! Anzi, ce n'è uno per ogni poligono a partire dal quadrilatero. E trovarlo non mi sembra affatto facile... E sto ancora indagando...
Seconda animazione: ecco infiniti
triangoli scaleni simili, in progressione geometrica, che tassellano un
pentagono. - poligonali regolari - triangoli simili - auto-similitudine - gnomone - tassellazione regolare del piano Quarta animazione: infiniti triangoli simili tassellano un esagono Quinta animazione: è la volta della tassellazione dell'ettagono Sesta animazione: il triangolo scaleno è lo gnomone dell'ottagono Settima animazione: appare il mollusco con tanto di spirale logaritmica!" |
|||||
|
Reputo interessante riportare una riflessione di Giorgio Pietrocola, che scrive: "Sto ancora pensando ai miei triangoli scaleni (evidenziati nelle precedenti animazioni), perché credo avrebbero interessato moltissimo Escher, che però, sospetto, non li abbia mai conosciuti. Ecco una laboriosa animazione (clicca qui per vederla) a sostegno della mia affermazione." |
|||||
|
AGGIORNAMENTO (15/07/2004) Giorgio Pietrocola, che ringrazio, ha aggiornato il suo file relativo a "Studio di poligonali regolari aventi lati in progressione geometrica e delle relative curve interpolanti eseguito con l' aiuto della fida tartaruga e della sua geometria." ( CLICCATE QUI ) |
|||||
|
AGGIORNAMENTO (05/08/2004) ( CLICCATE QUI ) |
|||||
|
|||||




 la quarta animazione
la quarta animazione